之前的博客:中简单介绍了Learning to Rank的基本原理,也讲到了Learning to Rank的几类常用的方法:pointwise,pairwise,listwise。这篇博客就很多公司在实际中通常使用的pairwise的方法进行介绍,首先我们介绍相对简单的 RankSVM 和 IR SVM。
1. RankSVM
RankSVM的基本思想是,将排序问题转化为pairwise的分类问题,然后使用SVM分类模型进行学习并求解。
1.1 排序问题转化为分类问题
对于一个query-doc pair,我们可以将其用一个feature vector表示:x。而排序函数为f(x),我们根据f(x)的大小来决定哪个doc排在前面,哪个doc排在后面。即如果f(xi) > f(xj),则xi应该排在xj的前面,反之亦然。可以用下面的公式表示:
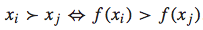
理论上,f(x)可以是任意函数,为了简单起见,我们假设其为线性函数: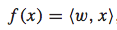 。
。
如果这个排序函数f(x)是一个线性函数,那么我们便可以将一个排序问题转化为一个二元分类问题。理由如下:
首先,对于任意两个feature vector xi和 xj,在f(x)是线性函数的前提下,下面的关系都是存在的:
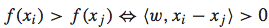
然后,便可以对xi和 xj的差值向量考虑二元分类问题。特别地,我们可以对其赋值一个label:
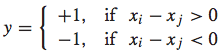

1.2 SVM模型解决排序问题
将排序问题转化为分类问题之后,我们便可以使用常用的分类模型来进行学习,这里我们选择了Linear SVM,同样的,可以通过核函数的方法扩展到 Nonlinear SVM。
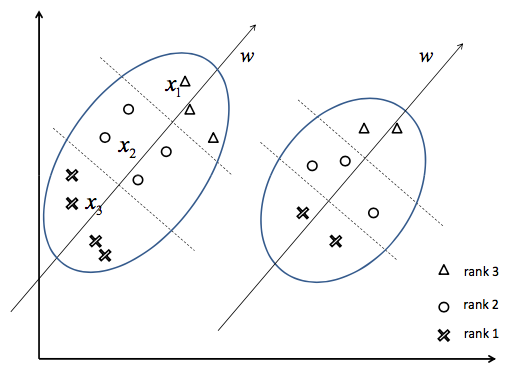
如下面左图所示,是一个排序问题的例子,其中有两组query及其相应的召回documents,其中documents的相关程度等级分为三档。而weight vector w对应了排序函数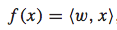 ,可以对query-doc pair进行打分和排序。
,可以对query-doc pair进行打分和排序。
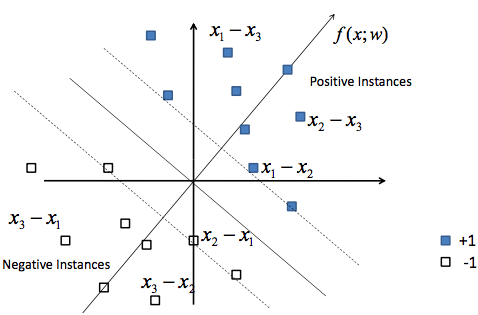
而下面右图则展示了如何将排序问题转化为分类问题。在同一个组内(同一个query下)的不同相关度等级的doc的feature vector可以进行组合,形成新的feature vector:x1-x2,x1-x3,x2-x3。同样的,label也会被重新赋值,例如x1-x2,x1-x3,x2-x3这几个feature vector的label被赋值成分类问题中的positive label。进一步,为了形成一个标准的分类问题,我们还需要有negative samples,这里我们就使用前述的几个新的positive feature vector的反方向向量作为相应的negative samples:x2-x1,x3-x1,x3-x2。另外,需要注意的是,我们在组合形成新的feature vector的时候,不能使用在原始排序问题中处于相同相似度等级的两个feature vector,也不能使用处于不同query下的两个feature vector。
1.2 SVM模型的求解过程
转化为了分类问题后,我们便可以使用SVM的通用方式进行求解。首先我们可以得到下面的优化问题:
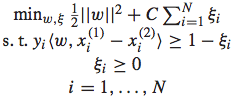
通过将约束条件带入进原始优化问题的松弛变量中,可以进一步转化为非约束的优化问题:
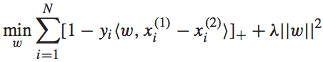
加和的第一项代表了hinge loss,第二项代表了正则项。primal QP problem较难求解,如果使用通用的QP解决方式则费时费力,我们可以将其转化为dual problem,得到一个易于求解的形式:
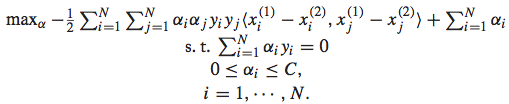
而最终求解得到相应的参数后,排序函数可以表示为:
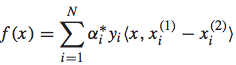
于是,RankSVM方法求解排序问题的步骤总结起来,如下图所示:

2. IR SVM
2.1 loss function的改造
上面介绍的RankSVM的基本思想是,将排序问题转化为pairwise的分类问题,然后使用SVM分类模型进行学习并求解。所以其在学习过程中,是使用了0-1分类损失函数(虽然实际上是用的替换损失函数hinge loss)。而这个损失函数的优化目标跟Information Retrieval的Evaluation常用指标(不仅要求各个doc之间的相对序关系正确,而且尤其重视Top的doc之间的序关系)还是存在gap的。所以有研究人员对此进行了研究,通过对RankSVM中的loss function进行改造从而使得优化目标更好地与Information Retrieval问题的常用评价指标相一致。
首先,我们通过一些例子来说明RankSVM在应用到文本排序的时候遇到的一些问题,如下图所示。

第一个问题就是,直接使用RankSVM的话,会将不同相似度等级的doc同等看待,不会加以区分。这在具体的问题中又会有两种形式:
1)Example 1中,3 vs 2 和 3 vs 1的两个pair,在0-1 loss function中是同等看待的,即它们其中任一对的次序的颠倒对loss function的增加大小是一样的。而这显然是不合理的,因为3 vs 1的次序颠倒显然要比 3 vs 2的次序的颠倒要更加严重,需要给予不同的权重来区分。
2)Example 2中,ranking-1是position 1 vs position 2的两个doc的位置颠倒了,ranking-2是position 3 vs position 4的两个doc的位置颠倒了,这两种情况在0-1 loss function中也是同等看待的。这显然也是不合理的,由于IR问题中对于Top doc尤其重视,ranking-1的问题要比ranking-2的问题更加严重,也是需要给予不同的权重加以区分。
第二个问题是,RankSVM对于不同query下的doc pair同等看待,不会加以区分。而不同query下的doc的数目是很不一样的。如Example 3所示,query-4的doc书目要更多,所以在训练过程中,query-4下的各个doc pair的训练数据对于模型的影响显然要比query-3下的各个doc pair的影响更大,所以最终结果的模型会有bias。
IR SVM针对以上两个问题进行了解决,它使用了cost sensitive classification,而不是0-1 classification,即对通常的hinge loss进行了改造。具体来说,它对来自不同等级的doc pair,或者来自不同query的doc pair,赋予了不同的loss weight:
1)对于Top doc,即相似度等级较高的doc所在的pair,赋予较大的loss weight。
2)对于doc数目较少的query,对其下面的doc pair赋予较大的loss weight。

2.2 IR SVM的求解过程
IR SVM的优化问题可以表示如下:
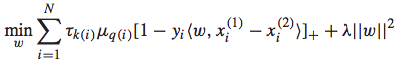
其中,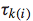 代表了隶属于第k档grade pair的instance的loss weight值。这个值的确定有一个经验式的方法:对隶属于这一档grade pair的两个doc,随机交换它们的排序位置,看对于NDCG@1的减少值,将所有的减少值求平均就得到了这个loss weight。可以想象,这个loss weight值越大,说明这个pair的doc对于整体评价指标的影响较大,所以训练时候的重要程度也相应较大,这种情况一般对应着Top doc,这样做就是使得训练结果尤其重视Top doc的排序位置问题。反之亦然。
代表了隶属于第k档grade pair的instance的loss weight值。这个值的确定有一个经验式的方法:对隶属于这一档grade pair的两个doc,随机交换它们的排序位置,看对于NDCG@1的减少值,将所有的减少值求平均就得到了这个loss weight。可以想象,这个loss weight值越大,说明这个pair的doc对于整体评价指标的影响较大,所以训练时候的重要程度也相应较大,这种情况一般对应着Top doc,这样做就是使得训练结果尤其重视Top doc的排序位置问题。反之亦然。
而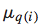 这个参数则对应了query的归一化系数。可以表示为
这个参数则对应了query的归一化系数。可以表示为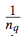 ,即该query下的doc数目的倒数,这个很好理解,如果这个query下的doc数目较少,则RankSVM训练过程中相对重视程度会较低,这时候通过增加这个权重参数,可以适当提高这个query下的doc pair的重要程度,使得模型训练中能够对不同的query下的doc pair重视程度相当。
,即该query下的doc数目的倒数,这个很好理解,如果这个query下的doc数目较少,则RankSVM训练过程中相对重视程度会较低,这时候通过增加这个权重参数,可以适当提高这个query下的doc pair的重要程度,使得模型训练中能够对不同的query下的doc pair重视程度相当。
IR SVM的优化问题如下:
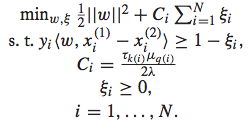
同样地,也需要将其转化为dual problem进行求解:
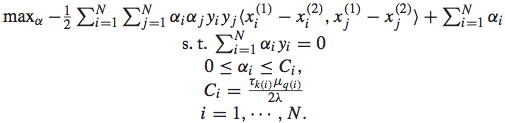
而最终求解得到相应的参数后,排序函数可以表示为:
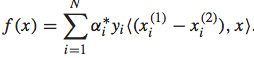
于是,IR SVM方法求解排序问题的步骤总结起来,如下图所示:

版权声明:
本文由所有,发布于。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。